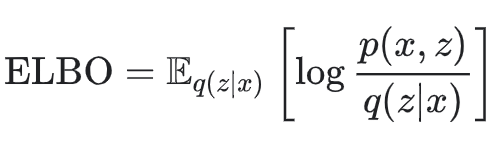ELBO - Evidence Lower Bound

Posted on *  •  2 minutes  • 384 words

Intractable Posterior

Latent variables are a transformation of the data points into a continuous lower-dimensional space. A latent variable model involves the evaluation of the posterior distribution $p(z|x)$ of the latent variables $z$ given the observed variables $x$.

The posterior distribution can be obtained by using Baye’s rule

$$ p_{\theta}(z|x) = \frac{p_{\theta}(x|z)p_{\theta}(z)}{p_{\theta}(x)} $$

with,

• The prior distribution $p(z)$ of the latent variables.
• The likelihood $p(x|z)$ defines the mapping of latent variables to $x$.
• The normalizing constant $p(x)$ or marginal likelihood or evidence is the distribution of the original data.
• Joint distribution $p(x,z) = p(x|z)p(z)$ multiplication of the likelihood and the prior and essentially describes our model.

It often happens in real life, even with simple priors and likelihood functions, calculating the exact posterior distribution becomes intractable in high dimensions. To overcome this issue, instead of calculating the exact posterior several approximation methods are used.

• Sampling based methods such as Monte Carlo methods and Markov Chain Monte Carlo methods.
• Variational methods.

Variational Method

The main idea behind variational methods is to approximate the intractable distribution $p_\theta(z|x)$ with another distribution $q_\phi (z|x)$ from where we are able to sample from. To quantify the difference between the two distributions, we minimize Reverse KL Divergence (expected log likelihood ratio) between the two: $$ D_{KL}(q_\phi||p_\theta) = \mathbb{E_{q\phi}}\left[log\frac{q_\phi(z|x)}{p_\theta(z|x)}\right] $$

The intractable $p_\theta(z|x)$ can be rewritten using Bayes rule:

$$ D_{KL}(q_\phi||p_\theta) = \mathbb{E_{q\phi}}[log(q_\phi(z|x))] - \mathbb{E_{q\phi}}[log(p_\theta(z|x))] $$ and using joint probablity $$ D_{KL}(q_\phi||p_\theta) = \mathbb{E_{q\phi}}[log(q_\phi(z|x))] - \mathbb{E_{q\phi}}\left[ log \frac {p_\theta(z,x)}{p_\theta(x)} \right] $$

Expanding the last term and writing in integral form $$ D_{KL}(q_\phi||p_\theta) = \mathbb{E_{q\phi}}[log(q_\phi(z|x))] - \mathbb{E_{q\phi}}[\mathop{log} p_\theta(z,x)] + \mathop{log} p_\theta(x)\int q_\phi(z|x)dz $$

Since, integral of a density function is 1, leaving only the marginal log likelihood in the last term $$ D_{KL}(q_\phi||p_\theta) = \mathbb{E_{q\phi}}[log(q_\phi(z|x))] - \mathbb{E_{q\phi}}[\mathop{log} p_\theta(z,x)] + \mathop{log} p_\theta(x) $$

Since $D_{KL}(q_\phi||p_\theta) \geq 0$, we can rewrite marginal log likelihood or log Evidence as $$ \mathop{log} p_\theta(x) \geq - \mathbb{E_{q\phi}}[\mathop{log}q_\phi(z|x)] + \mathbb{E_{q\phi}}[\mathop{log} p_\theta(z,x))] $$ where, the right hand side being its **lower bound**. Maximizing lower bound would mean minimizng the $D_{KL}(q_\phi||p_\theta)$

Evidence Lower BOund (ELBO)

$$ ELBO = - \mathbb{E_{q\phi}}[\mathop{log}q_\phi(z|x)] + \mathbb{E_{q\phi}}[\mathop{log} p_\theta(z,x))] $$

$$ = - \mathbb{E_{q\phi}}[\mathop{log}q_\phi(z|x)] + \mathbb{E_{q\phi}}[\mathop{log} p_\theta(x|z))] + \mathbb{E_{q\phi}}[\mathop{log} p_\theta(z))] $$ $$ = \mathbb{E_{q\phi}}[\mathop{log} p_\theta(x|z))] - \mathbb{E_{q\phi}}\left[log \frac{q_\phi(z|x)} {p_\theta(z)} \right] $$

with

ELBO = Expected reconstruction Error - KL Divergence between approx posterior and the prior.