Graph Isomorphism Network
Posted on * • 3 minutes • 504 words
Graph neural networks (GNN) rely on graph operations that include neural network training for various graph related tasks. GNNs only learn node embeddings. To predict the properties of the entire molecules as graph, it is important to learn an entire graph embedding. GIN was designed to maximize the representational (or discriminative) power of a GNN. Graph Isomorphism Network (GIN) designed by Xu et al., 2018a, which was recently proposed to implement Weisfeiler-Lehman (WL) graph isomorphism test, a classical algorithm used to test if two graphs are isomorphic.
GNN is not Injective
In GNN and GraphSAGE, the problem is with the aggregation functions. A layer of a GNN consists of an aggregate (message) function and a combine (update) function Two common aggregation methods are mean pooling and max pooling which are although invariant under node permutation but fail on some graphs.
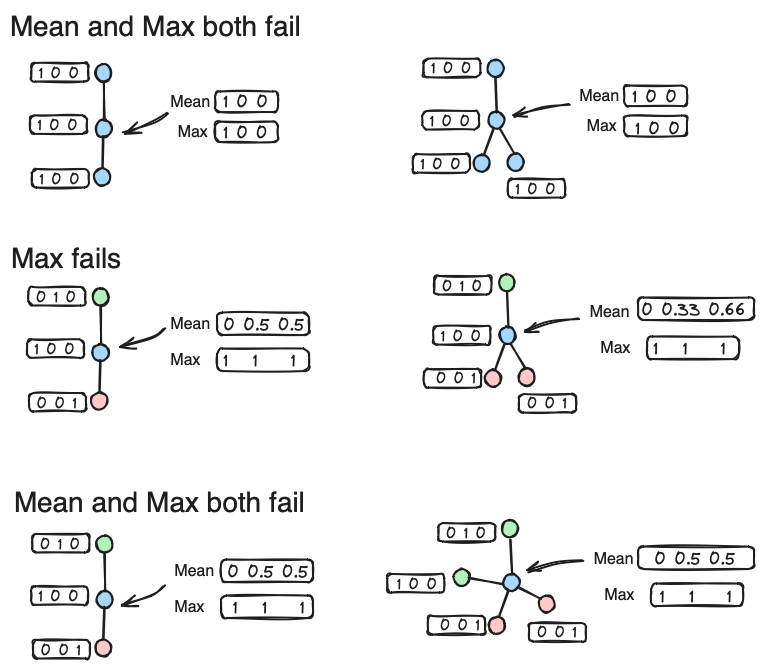
I needs an aggregation mechanism through the computational graph is injective to get different outputs for different computation graphs.
Weisfeiler-Lehman test
Are two graphs topologically identical?
WL test done iteratively:
- Aggregate the labels of nodes and their neighbors,
- hashes the aggregated labels into unique new labels.
The algorithm decides that two graphs are non-isomorphic if at some iteration the labels of the nodes between two graphs differ. So if GNN can map two graphs $G_1$ and $G_2$ to different embedings, then WL test also decides $G_1$ and $G_2$ are non-isomorphic.
How to maximize expressiveness of GNN
In paper “How Powerful are Graph Neural Networks?” they state that, if the neighbor aggregation and graph-level readout functions are injective, then the resulting GNN is as powerful as the WL test.

In a GNN, in the kth iteration we have:
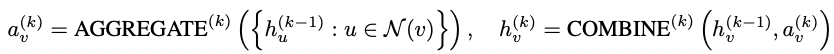
In a GIN, we still have the same steps, with $AGGREGATE$ is a $\sum$, and add tiny bit variation to current node and the push it through a non linear function, MLP, could be multiple layers.
$$ h_{v}^{k} = MLP^{k}\left ( \left ( 1+\epsilon^k \right )\cdot h_v^{(k-1)}+ \sum_{u\in N(v)}h_u^{(k-1)} \right ) $$
$$ h_G = CONCAT \left ( READOUT \left ( \left\{ h_{v}^{k} | v \in G \right\} \right ) \mid k = 0,1, \cdots ,k \right ) $$
Then $READOUT$ operation is done for every layer and concatenate to represent the entire graph. It turns out that the discriminative and representational power of GIN is equal to the power of the Weisfeiler-Lehman test. The WL test iteratively (1) aggregates the labels of nodes and their neighborhoods, and (2) hashes the aggregated labels into unique new labels. The algorithm decides that two graphs are non-isomorphic if at some iteration the labels of the nodes between the two graphs differ.
A walkthrough
Taken from Kim B-H and Ye JC (2020) Understanding Graph Isomorphism Network for rs-fMRI Functional Connectivity Analysis. Front. Neurosci. 14:630. doi: 10.3389/fnins.2020.00630
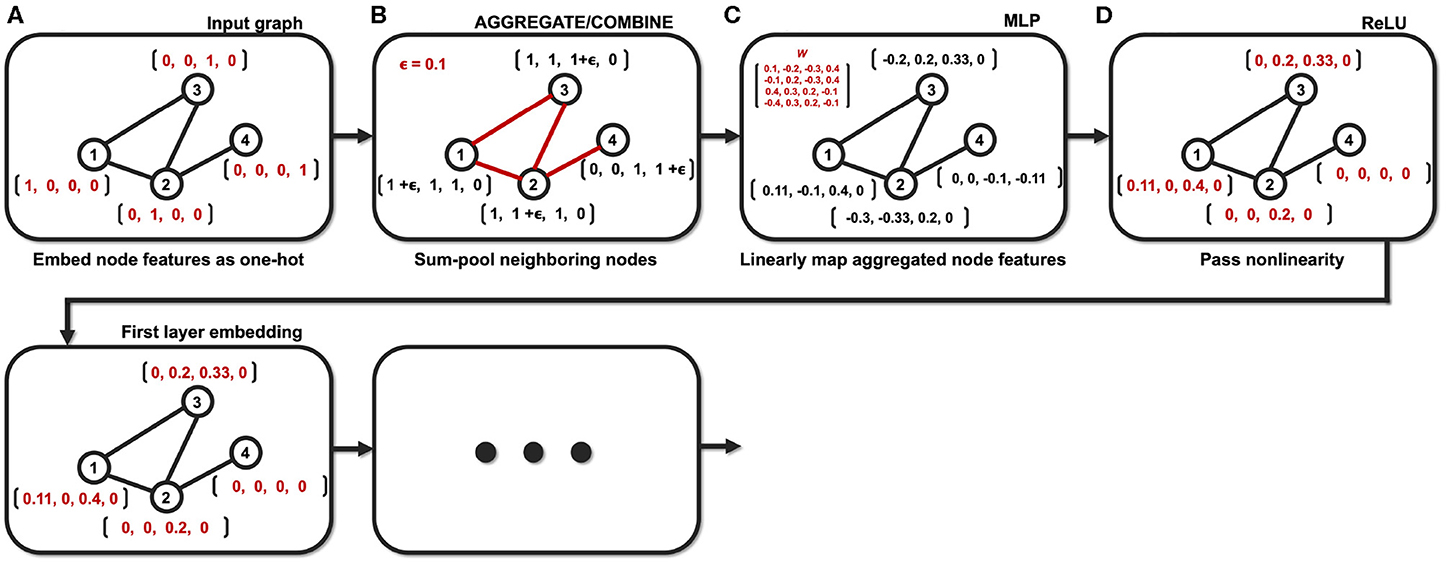
Example of the GIN operation with a small graph (N = 4). (A) Node features are embedded as one-hot vectors. (B) Neighboring nodes are aggregated/combined. (C) Aggregated node features are mapped with learnable parameters. (D) Mapped node features are passed through nonlinear activation function.