Message Passing in Graph Conv Network

Posted on * • 3 minutes • 563 words

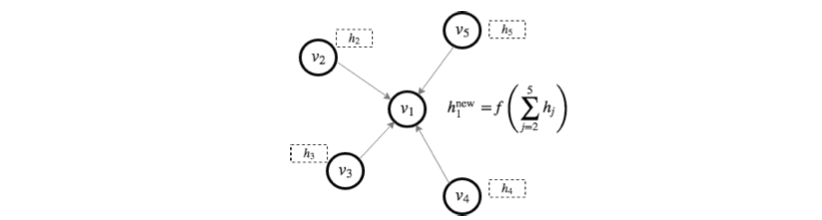
Message Passing

Its an iterative scheme of updating node representations based on the aggregation from nearby nodes.

Suppose $h_{u}^{k}$ represents the node embeddings for some node at iteration $k$, then at $k+1$, the following was orginally proposed for GNN

$ h_{u}^{(k+1)} = σ (W_{self}^{k+1} h_{u}^{k} + W_{neigh}^{k+1} Σ_{neigh} h_{v}^{k}) $

Collapsing $W_{self}$ and $W_{neigh}$ by adding self-loops to Adjacency matrix:

$ H^{(k+1)} = σ (W^{k+1}(A + I) H^{k} ) $

Coming from GCN perspective, Kipf and Welling 2016, proposed follwing: $ H^{(k+1)} = σ (W^{k+1}\hat{A} H^{k}) $

where, $ \hat{A} = (D+I)^{-1/2}(I+A)(D+I)^{-1/2} $ that Normalizes $A$ by # of nodes in neighborhood and $D$ is the degree matrix

Lets look at it with code

import numpy as np
import networkx as nx
from scipy.linalg import sqrtm

# Adjacencey matrix
A = np.array(
    [[0, 0, 1, 0, 1],
     [0, 0, 0, 0, 1],
     [0, 0, 0, 1, 1],
     [0, 0, 1, 0, 1],
     [1, 1, 0, 0, 0]]
)

g = nx.from_numpy_array(A)
A_tilde = A + np.eye(g.number_of_nodes())
A_tilde

array([[1., 0., 1., 0., 1.],
       [0., 1., 0., 0., 1.],
       [0., 0., 1., 1., 1.],
       [0., 0., 1., 1., 1.],
       [1., 1., 0., 0., 1.]])

D_tilde = np.zeros_like(A_tilde)
np.fill_diagonal(D_tilde, np.asarray(A_tilde.sum(axis=1)).flatten())

D_tilde_invroot = np.linalg.inv(sqrtm(D_tilde))
D_tilde_invroot

array([[0.57735027, 0.        , 0.        , 0.        , 0.        ],
       [0.        , 0.70710678, 0.        , 0.        , 0.        ],
       [0.        , 0.        , 0.57735027, 0.        , 0.        ],
       [0.        , 0.        , 0.        , 0.57735027, 0.        ],
       [0.        , 0.        , 0.        , 0.        , 0.57735027]])

A_hat = D_tilde_invroot @ A_tilde @ D_tilde_invroot
A_hat

array([[0.33333333, 0.        , 0.33333333, 0.        , 0.33333333],
       [0.        , 0.5       , 0.        , 0.        , 0.40824829],
       [0.        , 0.        , 0.33333333, 0.33333333, 0.33333333],
       [0.        , 0.        , 0.33333333, 0.33333333, 0.33333333],
       [0.33333333, 0.40824829, 0.        , 0.        , 0.33333333]])

Implement GCN using Pytorch

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim

import torch
import torch.nn as nn
import torch.nn.functional as F

class GCNLayer(nn.Module):
    """
        GCN layer

        Args:
            input_dim (int): Dimension of the input
            output_dim (int): Dimension of the output (a softmax distribution)
            A (torch.Tensor): 2D adjacency matrix
    """

    def __init__(self, input_dim: int, output_dim: int, A: torch.Tensor):
        super(GCNLayer, self).__init__()
        self.input_dim = input_dim
        self.output_dim = output_dim
        self.A = A

        # A_hat = A + I
        self.A_hat = self.A + torch.eye(self.A.size(0))

        # Create diagonal degree matrix D using another way
        self.ones = torch.ones(input_dim, input_dim)
        self.D = torch.matmul(self.A.float(), self.ones.float())

        # Extract the diagonal elements
        self.D = torch.diag(self.D)

        # Create a new tensor with the diagonal elements and zeros elsewhere
        self.D = torch.diag_embed(self.D)

        # Create D^{-1/2}
        self.D_neg_sqrt = torch.diag_embed(torch.diag(torch.pow(self.D, -0.5)))

        # Initialise the weight matrix as a parameter
        self.W = nn.Parameter(torch.rand(input_dim, output_dim))

    def forward(self, X: torch.Tensor):

        # D^-1/2 * (A_hat * D^-1/2)
        support_1 = torch.matmul(self.D_neg_sqrt, torch.matmul(self.A_hat, self.D_neg_sqrt))

        # (D^-1/2 * A_hat * D^-1/2) * (X * W)
        support_2 = torch.matmul(support_1, torch.matmul(X, self.W))

        # ReLU(D^-1/2 * A_hat * D^-1/2 * X * W)
        H = F.relu(support_2)

        return H

# Example Usage
input_dim = 3  # Assuming the input dimension is 3
output_dim = 2  # Assuming the output dimension is 2

# Example adjacency matrix
A = torch.tensor([[1., 0., 0.],
                  [0., 1., 1.],
                  [0., 1., 1.]])

# Create the GCN Layer
gcn_layer = GCNLayer(input_dim, output_dim, A)

# Example input feature matrix
X = torch.tensor([[1., 2., 3.],
                  [4., 5., 6.],
                  [7., 8., 9.]])
# Forward pass
output = gcn_layer(X)

print("Otput Feat", output)

Otput Feat tensor([[ 8.4075,  2.2147],
        [18.6713,  4.6855],
        [21.7627,  5.4416]], grad_fn=<ReluBackward0>)