Transformer Encoder from Scratch
Posted on * • 9 minutes • 1788 words
Transformer Encoder from Scratch (with UmarJamil)
In a Transformer architecture, the encoder block is responsible for processing the input sequence. It consists of several layers, typically composed of self-attention mechanisms and feed-forward neural networks.
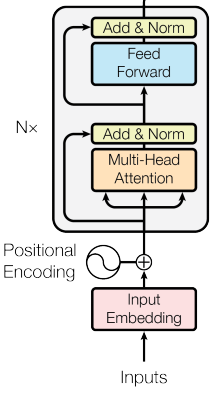
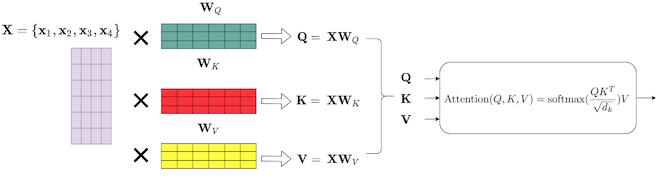
- Self-Attention Layer: This layer computes the attention scores between each position in the input sequence, allowing the model to weigh the importance of different tokens when encoding information. It helps capture dependencies between words in the sequence.
- Feed-Forward Neural Network: After the self-attention layer, the output is passed through a position-wise feed-forward neural network (FFNN). This network applies linear transformations followed by a non-linear activation function (such as ReLU) independently at each position in the sequence.
- Residual Connection and Layer Normalization: Both the self-attention layer and the feed-forward network are typically followed by a residual connection, which adds the input of the block to its output. This helps mitigate the vanishing gradient problem during training. Layer normalization is then applied to stabilize the training process. The encoder block processes the input sequence iteratively, with each block capturing different aspects of the input data. The output of the encoder is then passed to the decoder block for further processing in sequence-to-sequence tasks such as machine translation.
# IMport necessary libraries
# PyTorch
import torch
import torch.nn as nn
from torch.utils.data import Dataset, DataLoader, random_split
from torch.utils.tensorboard import SummaryWriter
# Math
import math
# HuggingFace libraries
! pip install transformers datasets
from datasets import load_dataset
# HuggingFace libraries
from tokenizers import Tokenizer
from tokenizers.models import WordLevel
from tokenizers.trainers import WordLevelTrainer
from tokenizers.pre_tokenizers import Whitespace
# Pathlib
from pathlib import Path
# typing
from typing import Any
# Library for progress bars in loops
from tqdm import tqdm
# Importing library of warnings
import warnings
Input Embedding
- A sentence that gets split into tokens
- Tokes numbers — are transformed into the vector embeddings.
# Creating Input Embeddings
class InputEmbeddings(nn.Module):
'''
d_model : Dimension of vectors (512)
vocab_size : Size of the vocabulary
Embedding : # PyTorch layer that converts integer indices to dense embeddings
'''
def __init__(self, d_model: int, vocab_size: int):
super().__init__()
self.d_model = d_model
self.vocab_size = vocab_size
self.embedding = nn.Embedding(vocab_size, d_model)
def forward(self, x):
# Normalizing the variance of the embeddings
return self.embedding(x) * math.sqrt(self.d_model)
Positional Encoding
Provides information about the relative or absolute position of the tokens in the sequence.
create a matrix (seq_len, d_model) filling it with 0s.We will then apply the sine function to even indices of the positional encoding matrix while the cosine function is applied to the odd ones.
Even indices (2i)
$ PE(pos, 2i) = sin(\frac{pos}{10000^{2i/d_{model}}}) $
Odd indices (2i+1)
$ PE(pos, 2i+1) = cos(\frac{pos}{10000^{2i/d_{model}}}) $
# Creating the Positional Encoding
class PositionalEncoding(nn.Module):
def __init__(self, d_model: int, seq_len: int, dropout: float) -> None:
super().__init__()
self.d_model = d_model # Dimensionality of the model
self.seq_len = seq_len # Maximum sequence length
self.dropout = nn.Dropout(dropout) # Dropout layer to prevent overfitting
# Creating a positional encoding matrix of shape (seq_len, d_model) filled with zeros
pe = torch.zeros(seq_len, d_model)
# Creating a tensor representing positions (0 to seq_len - 1)
position = torch.arange(0, seq_len, dtype = torch.float).unsqueeze(1) # Transforming 'position' into a 2D tensor['seq_len, 1']
# Creating the division term for the positional encoding formula
div_term = torch.exp(torch.arange(0, d_model, 2).float() * (-math.log(10000.0) / d_model))
# Apply sine to even indices in pe
pe[:, 0::2] = torch.sin(position * div_term)
# Apply cosine to odd indices in pe
pe[:, 1::2] = torch.cos(position * div_term)
# Adding an extra dimension at the beginning of pe matrix for batch handling
pe = pe.unsqueeze(0)
# Registering 'pe' as buffer. Buffer is a tensor not considered as a model parameter
self.register_buffer('pe', pe)
def forward(self,x):
# Addind positional encoding to the input tensor X
x = x + (self.pe[:, :x.shape[1], :]).requires_grad_(False)
return self.dropout(x) # Dropout for regularization
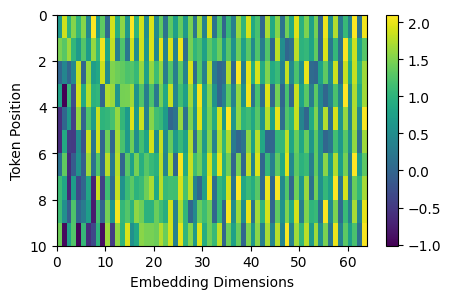
tokens = 10
dimensions = 64
pos_encoding = PositionalEncoding(dimensions, tokens,0.05)
x = torch.rand(1,10,64)
pos_enc = pos_encoding.forward(x)
import matplotlib.pyplot as plt
plt.figure(figsize=(5,3))
plt.pcolormesh(pos_enc[0], cmap='viridis')
plt.xlabel('Embedding Dimensions')
plt.xlim((0, dimensions))
plt.ylim((tokens,0))
plt.ylabel('Token Position')
plt.colorbar()
plt.show()
Layer Normalization
The normalization layers called Add & Norm. During its forward pass, we compute the mean and standard deviation of the input data. We then normalize the input data by subtracting the mean and dividing by the standard deviation plus a small number called epsilon to avoid any divisions by zero. This process results in a normalized output with a mean 0 and a standard deviation 1. We will then scale the normalized output by a learnable parameter alpha and add a learnable parameter called bias.
# Creating Layer Normalization
class LayerNormalization(nn.Module):
def __init__(self, eps: float = 10**-6) -> None: # We define epsilon as 0.000001 to avoid division by zero
super().__init__()
self.eps = eps
# We define alpha as a trainable parameter and initialize it with ones
self.alpha = nn.Parameter(torch.ones(1)) # One-dimensional tensor that will be used to scale the input data
# We define bias as a trainable parameter and initialize it with zeros
self.bias = nn.Parameter(torch.zeros(1)) # One-dimensional tenso that will be added to the input data
def forward(self, x):
mean = x.mean(dim = -1, keepdim = True) # Computing the mean of the input data. Keeping the number of dimensions unchanged
std = x.std(dim = -1, keepdim = True) # Computing the standard deviation of the input data. Keeping the number of dimensions unchanged
# Returning the normalized input
return self.alpha * (x-mean) / (std + self.eps) + self.bias
Feed Forward Network Block
We have two linear transformation layers—$self.linear_1$ and $self.linear_2$ —and the inner-layer $d_ff$. The input data with dimension $d_model$ will first pass through the $self.linear_1$ transformation, with output dimensionality to $d_ff$. And then ReLU activation and the $self.dropout$. Then the $self.linear_2$ transformation giving back the original $d_model$ dimension.
# Creating Feed Forward Layers
class FeedForwardBlock(nn.Module):
def __init__(self, d_model: int, d_ff: int, dropout: float) -> None:
super().__init__()
# First linear transformation
self.linear_1 = nn.Linear(d_model, d_ff) # W1 & b1
self.dropout = nn.Dropout(dropout) # Dropout to prevent overfitting
# Second linear transformation
self.linear_2 = nn.Linear(d_ff, d_model) # W2 & b2
def forward(self, x):
# (Batch, seq_len, d_model) --> (batch, seq_len, d_ff) -->(batch, seq_len, d_model)
return self.linear_2(self.dropout(torch.relu(self.linear_1(x))))
Multi-Head Attention
The Multi-Head Attention block receives the input data split into matrices $Q$, $K$, and $V$ with the same dimensions as the input.
Then multiplied by weight matrices $W^Q$, $W^K$ and $W^V$.
Next concatenate every head into an $H$ matrix, which is then transformed by another weight matrix $W_o$ to produce the multi-head attention output matrix $MH-A$ with input dimensionality.
# Creating the Multi-Head Attention block
class MultiHeadAttentionBlock(nn.Module):
def __init__(self, d_model: int, h: int, dropout: float) -> None: # h = number of heads
super().__init__()
self.d_model = d_model
self.h = h
# We ensure that the dimensions of the model is divisible by the number of heads
assert d_model % h == 0, 'd_model is not divisible by h'
# d_k is the dimension of each attention head's key, query, and value vectors
self.d_k = d_model // h # d_k formula, like in the original "Attention Is All You Need" paper
# Defining the weight matrices
self.w_q = nn.Linear(d_model, d_model) # W_q
self.w_k = nn.Linear(d_model, d_model) # W_k
self.w_v = nn.Linear(d_model, d_model) # W_v
self.w_o = nn.Linear(d_model, d_model) # W_o
self.dropout = nn.Dropout(dropout) # Dropout layer to avoid overfitting
@staticmethod
def attention(query, key, value, mask, dropout: nn.Dropout):# mask => When we want certain words to NOT interact with others, we "hide" them
d_k = query.shape[-1] # The last dimension of query, key, and value
# We calculate the Attention(Q,K,V) as in the formula in the image above
attention_scores = (query @ key.transpose(-2,-1)) / math.sqrt(d_k) # @ = Matrix multiplication sign in PyTorch
# Before applying the softmax, we apply the mask to hide some interactions between words
if mask is not None: # If a mask IS defined...
attention_scores.masked_fill_(mask == 0, -1e9) # Replace each value where mask is equal to 0 by -1e9
attention_scores = attention_scores.softmax(dim = -1) # Applying softmax
if dropout is not None: # If a dropout IS defined...
attention_scores = dropout(attention_scores) # We apply dropout to prevent overfitting
return (attention_scores @ value), attention_scores # Multiply the output matrix by the V matrix, as in the formula
def forward(self, q, k, v, mask):
query = self.w_q(q) # Q' matrix
key = self.w_k(k) # K' matrix
value = self.w_v(v) # V' matrix
# Splitting results into smaller matrices for the different heads
# Splitting embeddings (third dimension) into h parts
query = query.view(query.shape[0], query.shape[1], self.h, self.d_k).transpose(1,2) # Transpose => bring the head to the second dimension
key = key.view(key.shape[0], key.shape[1], self.h, self.d_k).transpose(1,2) # Transpose => bring the head to the second dimension
value = value.view(value.shape[0], value.shape[1], self.h, self.d_k).transpose(1,2) # Transpose => bring the head to the second dimension
# Obtaining the output and the attention scores
x, self.attention_scores = MultiHeadAttentionBlock.attention(query, key, value, mask, self.dropout)
# Obtaining the H matrix
x = x.transpose(1, 2).contiguous().view(x.shape[0], -1, self.h * self.d_k)
return self.w_o(x) # Multiply the H matrix by the weight matrix W_o, resulting in the MH-A matrix
Residual Connections
Skip connection, providing a shortcut for the gradient to flow through during backpropagation.
# Building Residual Connection
class ResidualConnection(nn.Module):
def __init__(self, dropout: float) -> None:
super().__init__()
self.dropout = nn.Dropout(dropout) # We use a dropout layer to prevent overfitting
self.norm = LayerNormalization() # We use a normalization layer
def forward(self, x, sublayer):
# We normalize the input and add it to the original input 'x'. This creates the residual connection process.
return x + self.dropout(sublayer(self.norm(x)))
A single Encoder Block
# Building Encoder Block
class EncoderBlock(nn.Module):
# This block takes in the MultiHeadAttentionBlock and FeedForwardBlock, as well as the dropout rate for the residual connections
def __init__(self, self_attention_block: MultiHeadAttentionBlock, feed_forward_block: FeedForwardBlock, dropout: float) -> None:
super().__init__()
# Storing the self-attention block and feed-forward block
self.self_attention_block = self_attention_block
self.feed_forward_block = feed_forward_block
self.residual_connections = nn.ModuleList([ResidualConnection(dropout) for _ in range(2)]) # 2 Residual Connections with dropout
def forward(self, x, src_mask):
# Applying the first residual connection with the self-attention block
x = self.residual_connections[0](x, lambda x: self.self_attention_block(x, x, x, src_mask)) # Three 'x's corresponding to query, key, and value inputs plus source mask
# Applying the second residual connection with the feed-forward block
x = self.residual_connections[1](x, self.feed_forward_block)
return x # Output tensor after applying self-attention and feed-forward layers with residual connections.
Encoder
An Encoder can have several Encoder Blocks stored in Encoders $self.layers$
# Building Encoder
# An Encoder can have several Encoder Blocks
class Encoder(nn.Module):
# The Encoder takes in instances of 'EncoderBlock'
def __init__(self, layers: nn.ModuleList) -> None:
super().__init__()
self.layers = layers # Storing the EncoderBlocks
self.norm = LayerNormalization() # Layer for the normalization of the output of the encoder layers
def forward(self, x, mask):
# Iterating over each EncoderBlock stored in self.layers
for layer in self.layers:
x = layer(x, mask) # Applying each EncoderBlock to the input tensor 'x'
return self.norm(x) # Normalizing output