UMAP - Uniform Manifold Approximation and Projection
Posted on * • 6 minutes • 1124 words
Simplex and Simplical Complexes
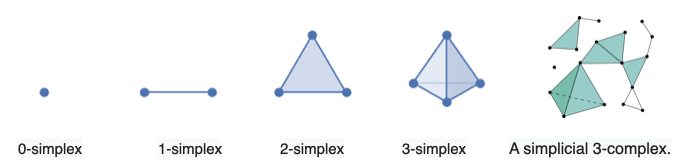
An $n$-simplex is a geometric object with $(n + 1)$ vertices which lives in an $n$-dimensional space.
- $0$-simplex (a $\sigma_0$ simplex ⟨$p0$⟩ generated by one point, $p0$)
- $1$-simplex (a $\sigma_1$ simplex ⟨$p0,p1$⟩ generated by two points, $p0$ and $p1$). A $1$-symplex is a line segment (including its end-points).
- $2$-simplex (a $\sigma_2$ simplex ⟨$p0, p1, p2$⟩ generated by three points, $p0$, $p1$, $p2$) A 2-simplex is a solid triangle (including its border).
- $3$-simplex (a $\sigma_3$ simplex ⟨$p0, p1, p2, p4$⟩ generated by three points, $p0$, $p1$, $p2$, $p4$)
 A simplicial complex $\mathcal {K}$ is a set of simplices that satisfies the following conditions:
A simplicial complex $\mathcal {K}$ is a set of simplices that satisfies the following conditions:
- Every face of a simplex from $\mathcal {K}$ is also in $\mathcal {K}$.
- The non-empty intersection of any two simplices $\sigma_1, \sigma_2 \in \mathcal {K}$ is a face of both $\sigma_1$ and $\sigma_2$.
Basically, simplical complex is a collection of simplices nicely put together and have no improper intersections. The second condition is also equivalent to that any pair of distinct simplices of $\mathcal {K}$ have disjoint interiors.
So, topological spaces can be constructed by gluing together simplices of various dimensions along their faces. One can use simplicial topology to for eg. approximately model surfaces. Triangular meshes (as commonly used in computer graphics) are just 2d simplicial complexes; as are Delaunay triangulations. A more restricted example of a simplicial complex is the notion of a hypergraph.
Cover and its Nerve
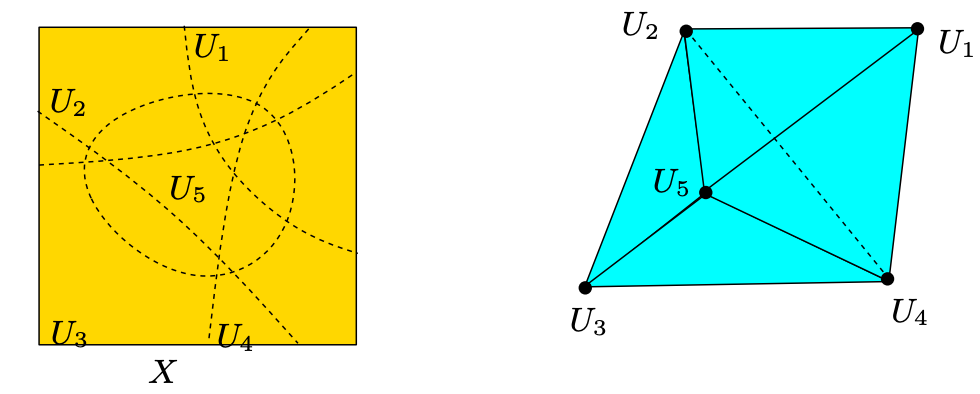 An open cover of a topological space $X$ is collection $\mathcal{U} = \{U_i\}_{i \in I}$ where $I$ is the
An open cover of a topological space $X$ is collection $\mathcal{U} = \{U_i\}_{i \in I}$ where $I$ is the
indexing set, such that $X = \{\cup_{i\in I} U_i\}$.
Given a cover $\mathcal U$ of a topological space $X$, its nerve $N(\mathcal{U})$ is the abstract simplical complex whose vertex set is $\mathcal U$ and such that
$$ \sigma = [{U_i}_0, {U_i}_1, \cdot\cdot\cdot, {U_i}_k] \in N(\mathcal U) $$
if and only if,
$$ \cap_{j=0}^{k} {U_i}_j \neq \emptyset $$
Čech Complex and the Vietoris-Rips Complex - Simplical Complexes from data
how one might construct a simplicial complex from a topological space
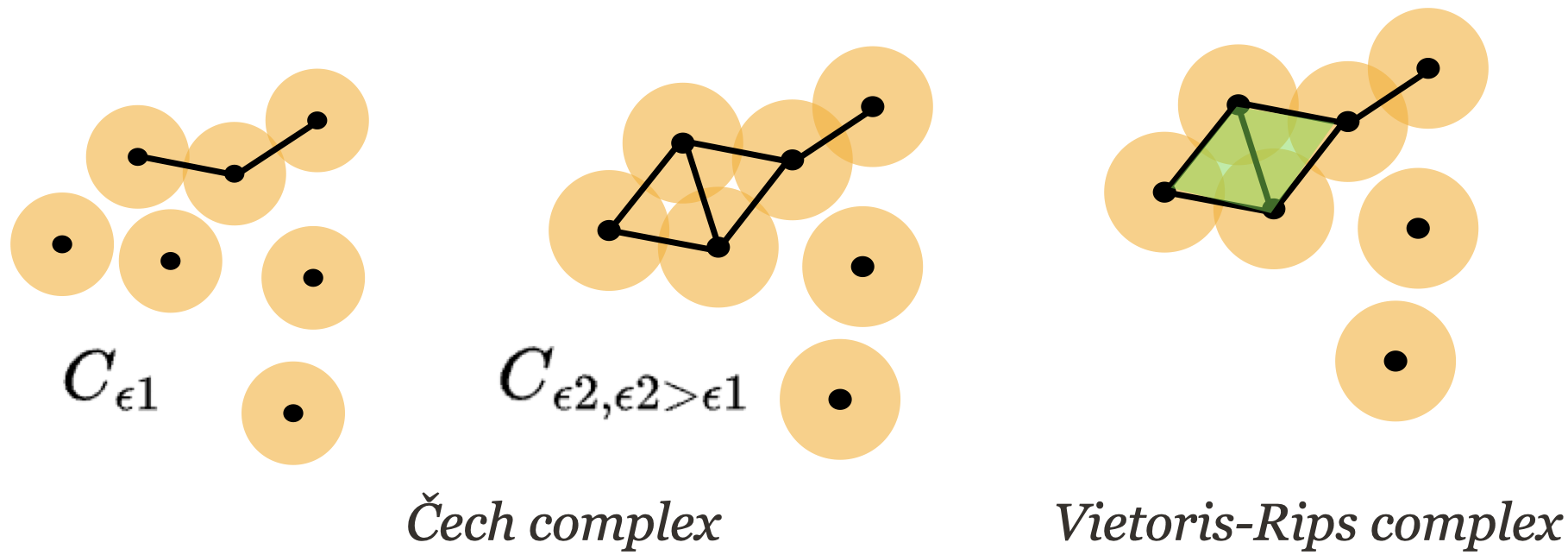 The Čech complex for a data set $X$ with radius $\epsilon \geq 0$, is defined as the simplical complex
The Čech complex for a data set $X$ with radius $\epsilon \geq 0$, is defined as the simplical complex
$$ C_{\epsilon}(X)= \{\sigma_I ∣ \cap_{i \in I}B_\epsilon(x_i) \neq \emptyset \} $$
Simply this means that we add a simplex $\sigma_I$ on vertices $\{x_i\}_{i \in I}$ when balls with radius $\epsilon$ around each vertex all have a nonempty intersection. The ball at each point gives the cover and the Čech complex is the nerve of this cover. Since the balls are convex (contractible), it is a good cover and its nerve captures the topolgy of the cover.
The Vietoris-Rips complex relaxes the Čech condition for simplex inclusion by allowing a simplex provided its vertices are pairwaise within distance $\epsilon$. Vietoris-Rips complexes are much easier to work with computationally,
Fuzzy topology
Uber metric space
An extended pseudo-metric space (or an extended pseudo-metric space, EPMet,) is a pair $(X, d)$, where $X$ is a set and $d : X \times X \to [0,\infty]$, such that for all $x,y,z \in X$,
$$ a) $d(x, x) = 0$,
b) $d(x, y) = d(y, x)$,
c) $d(x, z) \le d(x, y) + d(y, z)$. $$
EPMet lets distances be infinite ("pseudo"), and $d(x, y) = 0$ doe not imply that $x$ and $y$ coincide i.e., it lets distinct points have distance zero from each other. A metric space is an EPMet space for which $d(x, y) = 0$ implies $x = y$, and all distances $d(x, y)$ are finite.
Fuzzy simplicial set
A Set is any well defined collection of objects and has a binary value for membership. Fuzziness occurs when the boundary of a piece of information is not clear-cut. Fuzzy set theory is an extension of classical set theory where elements have degree of membership. A fuzzy simplicial set is a simplicial set in which every simplex has a strength. A simplex has strength at most the minimum of its faces. All degeneracies of a simplex have the same strength as the simplex. The category of fuzzy simplicial sets is denoted sFuzz.
David Spivak has shown how to turn a ‘fuzzy simplicial set’ into an ‘uber-metric space’ and back using category theory.
Let FinEPMet be the sub-category of EPMet whose objects are finite extended-pseudo-metric spaces. And further, let Fin-sFuzz be the subcategory of sFuzz consisting of the fuzzy simplicial sets with a finite number of non-degenerate simplices. The functors FinSing : FinEPMet $\to$ Fin-sFuzz and FinReal : Fin-sFuzz $\to$ FinEPMet form an adjunction FinReal FinEPMet.
So, we can now convert a set of datapoints $D$ to a family of elements of FinEPMet, and from that to a family of finite fuzzy simplicial sets FinSing$(D, d_{xi})$ for $x_i \in D$. And the fuzzy topology can be given by union of fuzzy sets.
UMAP
Thats all good. The data has a structure and likley sits on a manifold whose dimension is considerably lower than the ambient dimension and we can learn this manifold from data. Lets say we have the following nice data (left panel), we build covers with balls of unit radius and then construct a simplical complex - the graph, that reflects the topolgy.
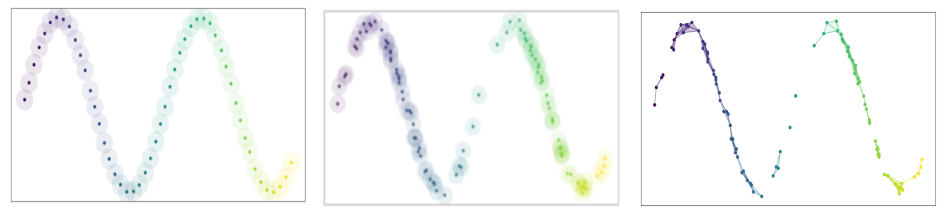 In real scenario (the right panels), the data is not uniformly distributed over the manifold. And so we have not exactly recovered the topology.
We assume following that the data is uniformly distributed on Riemannian manifold. The Riemannian metric is locally constant, or can be approximated as such. We contract and expand the manifold, by using different notion of distance, such that the data looks uniform. This would mean that at each point the unit-balls have different sizes in the ambient dimension and build a k-neighbor graph and assume the neighborhood to be flat.
In real scenario (the right panels), the data is not uniformly distributed over the manifold. And so we have not exactly recovered the topology.
We assume following that the data is uniformly distributed on Riemannian manifold. The Riemannian metric is locally constant, or can be approximated as such. We contract and expand the manifold, by using different notion of distance, such that the data looks uniform. This would mean that at each point the unit-balls have different sizes in the ambient dimension and build a k-neighbor graph and assume the neighborhood to be flat.
UMAP does not rely on a fixed radius balls to build cover, but rather uses fuzzy set theory to define a “fuzzy cover”. Assuming that the manifold is locally connected. That is one can‘t have a point that is completely separated from everything else. And that the fuzzy open set extends as far as its closest neighbor and then decays. This is implemented simply by an exponential decay $exp(-d_{i,j})$. And also, we have Riemaninan manifold with different distances. How to glue different metrics together?
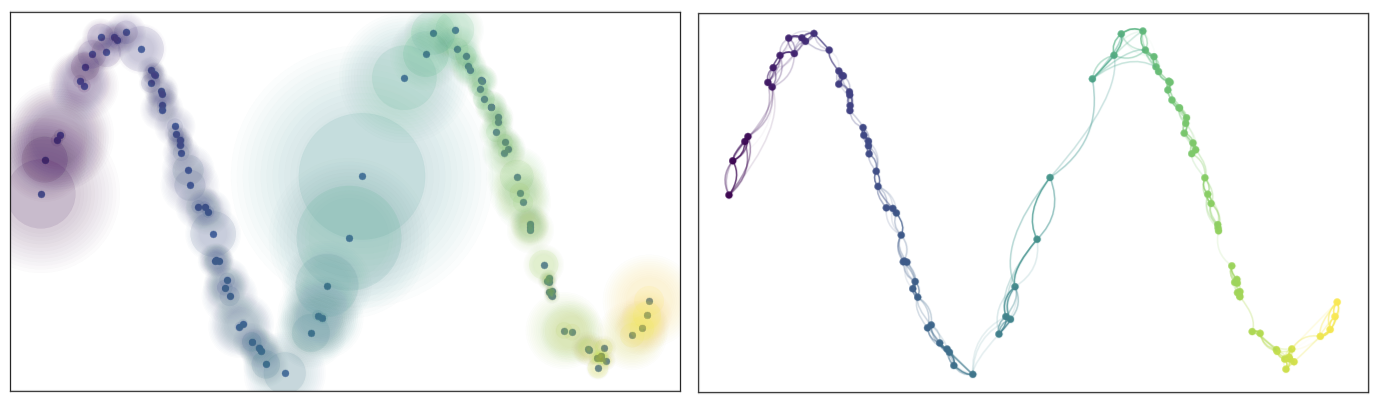 Using the fuzzy simplical sets for the above data we get a bi-directional weighted graph. This motivates the need for a symmetrization step through usage of one of the ways of fuzzy union via a t-conorm. it is defined as
$$
f(\alpha, \beta) = \alpha + \beta - \alpha \times \beta
$$
with $\alpha$ and $\beta$ are the edge weights.
Using the fuzzy simplical sets for the above data we get a bi-directional weighted graph. This motivates the need for a symmetrization step through usage of one of the ways of fuzzy union via a t-conorm. it is defined as
$$
f(\alpha, \beta) = \alpha + \beta - \alpha \times \beta
$$
with $\alpha$ and $\beta$ are the edge weights.
References
- Algorithms and Theory of Computation Handbook, Volume 2: Special Topics and Techniques, Edition 2 - Mikhail J. Atallah · Marina Blanton
- https://www.math.colostate.edu/~adams/teaching/dsci475spr2021/
- https://umap-learn.readthedocs.io/en/latest/how_umap_works.html
- https://www.uwo.ca/math/faculty/jardine/preprints/htpy-met4.pdf
- http://math.mit.edu/~dspivak/files/metric_realization.pdf - Metric realization of fuzzy simplicial sets.

