Model Selection - AIC and BIC

Posted on *  •  2 minutes  • 293 words

How to choose a best perfoming model?

Information criteria are used to measure the “quality” of a model by taking the goodness of fit and the complexity of the model into consideration. There are many information criteria to choose from, with two of the most well known information criteria are the AIC (Aikaike Information Criterion) (Akaike, 1973) and the BIC (Bayesian Information Criterion), (Schwarz, 1978).

Akaike’s Information Criterion (AIC)

AIC is basically the log-likelihood penalized by the number of parameters $K$ $$ AIC = -2log(\mathcal{L}(\hat{\theta}|y)) + 2K $$

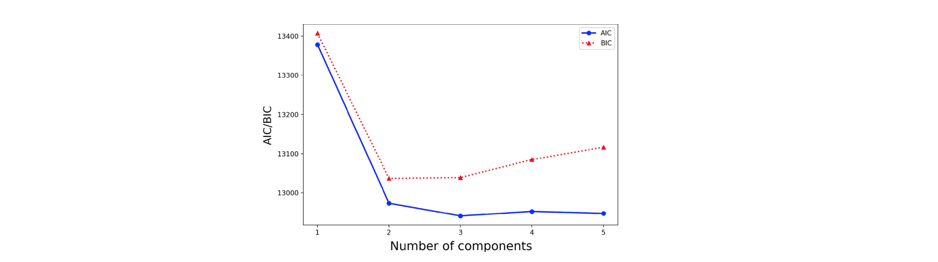
The lower the value for AIC, the better the fit of the model. The absolute value of the AIC value is not important. It can be positive or negative.

In general it is recommended to use the AIC if there is an emphasis on avoiding underfitting. The AIC is sensitive to the sample size ($n$), for a too small size the AIC tends to overfit and a stronger penalty term is recommended. For small sample sizes ($n/K \le 40$), use the second-order AIC: $$ AIC_c = -2(\mathcal{L}(\hat{\theta}|y)) + 2K + (2K+1)/(n-K-1) $$

Bayesian information criterion (BIC)

The Bayesian information criterion (BIC), also referred to as the Schwarz information criterion and Schwarz Bayesian. BIC imposes a greater penalty for the number of parameters than AIC. It is given by: $$ BIC = -2log(\mathcal{L}(\hat{\theta}|y)) + Klog(n) $$ The best model is the one that provides the minimum BIC.

To compare two models $M_i$ and $M_j$, one can use the BIC to estimate the Bayes factor Bij by $$ B_{ij} \approx exp(−\frac{1}{2}BIC_i + \frac{1}{2}BIC_j) $$ The candidate model with the smallest BIC value, is the candidate model with the highest Bayesian posterior probability. And therefore the “best” performing candidate model is the model with the lowest BIC value