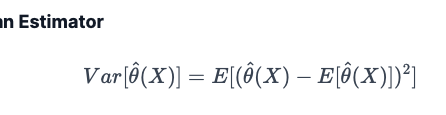Estimator, Bias & Variance

Posted on *  •  2 minutes  • 406 words

Parameter Characteristic/property calculated in population. Eg., mean ($\mu$), variance ($s^2$)

Statistic Characteristic/property calculated in sample. Eg., mean ($\bar{X}$), variance ($\sigma^2$). Mean is a function of the sample data. Sample mean:

$$\bar{X} = \frac{1}{N} \sum_{i=1}^{N} X_i$$

Expected Value The mean, expected value, or expectation, $\mathbb{E}(X)$ of a random variable $X$ is the long-term average of the random variable. That is, the mean of the $N$ values will be approximately equal to $\mathbb{E}(X)$ for large $N$.

In a probability distribution , the weighted average of possible values $x_i$ of a random variable, with weights given by their respective theoretical probabilities $P(x_i)$, is known as the expected value.

• Let $X$ be a discrete random variable with probability function $P(x_i)$

$$\mathbb{E}(X) = \sum_{}^{} x_i P(x_i)$$

• Let $X$ be a continuous random variable with probability density function $f(x)$

$$\mathbb{E}(X) = \int_{\infty }^{-\infty } xf(x)dx $$

Estimator and Estimation An estimator is a statistic (i.e., a function of the data), a rule for calculating the estimates about the population. If parameter is $\theta$, then estimator is $\hat{\theta}(X)$.

Estimator refers to a statistic if that statistic is used to estimate some parameter-of-interest. Let $X$ is a random variable from a population with distribution $P_\theta$, $\theta \in \Theta$. An example of parametric distribution function is the Normal distribution where the parameter vector $\theta = [\mu, \sigma]$ is unknown. The goal of the estimation procedure is to find a value $\hat{\theta}$ of the parameter $\theta$ so that the parameterized distribution $P_{\hat{\theta}}$ closely matches the distribution of data.

Estimate is a number that is the computed value of the estimator.

The target of an estimator does not necessarily have to be a particular “parameter” of a model: it can be any property of the model, such as a function of its parameters $g(\theta)$. For instance, $\mu^2$ is not a parameter for a normal $N(\mu, \sigma^2)$ model, but it can be estimated.

Bias of an Estimator A statistic is $\hat{\theta}(X)$ is said to be an unbiased estimator of $g(\theta)$ if and only if:

$$E[\hat{\theta}(X)] = g(\theta) \ \ \forall \theta \in \Theta $$

Otherwise, if

$$E[\hat{\theta}(X)] = g(\theta) + b(\theta) $$

then it is said to be a biased estimator with bias $b(\theta)$.

Variance of an Estimator

$$Var[\hat{\theta}(X)] = E[(\hat{\theta}(X) - E[\hat{\theta}(X)])^2 ] $$

and the standard error of the estimator is,

$$\hat{\sigma} = \sqrt{Var[\hat{\theta}(X)]}$$

• If the expected value of the estimator approaches the population value as the sample size increases, it is an asymptotically unbiased estimator.