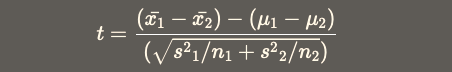Z-test and t-test
Posted on * • 2 minutes • 300 words
What is the Z Test?
z tests are a statistical way of testing a hypothesis when either:
- We know the population variance, or
- We do not know the population variance but our sample size is large n ≥ 30
If we have a sample size of less than 30 and do not know the population variance, then we must use a t-test.
One-Sample Z test
Compare a sample mean with the population mean. $$ t = \frac{\bar{x} - \mu}{\sigma / n}$$
Two Sample Z Test
Compare the mean of two samples. $$ t = \frac{(\bar{x_1} - \bar{x_2}) - (\mu_1 - \mu_2)}{(\sqrt{\sigma{^2}{_1}/n_1 + \sigma{^2}{_2}/n_2})}$$
What is the t-Test?
t-tests are a statistical way of testing a hypothesis when:
- We do not know the population variance
- Our sample size is small, n < 30
One-Sample t-Test
$$ t = \frac{\bar{x} - \mu}{s / n}$$ We perform a One-Sample t-test when we want to compare a sample mean with the population mean. The difference from the Z Test is that we do not have the information on Population Variance here. We use the sample standard deviation instead of population standard deviation in this case.
Two-Sample t-Test
We perform a Two-Sample t-test when we want to compare the mean of two samples.
$$ t = \frac{(\bar{x_1} - \bar{x_2}) - (\mu_1 - \mu_2)}{(\sqrt{s{^2}{_1}/n_1 + s{^2}{_2}/n_2})}$$
If the sample size is large enough, then the Z test and t-Test will conclude with the same results. For a large sample size, Sample Variance will be a better estimate of Population variance so even if population variance is unknown, we can use the Z test using sample variance.
Similarly, for a Large Sample, we have a high degree of freedom. And since t-distribution approaches the normal distribution**, the difference between the z score and t score is negligible.